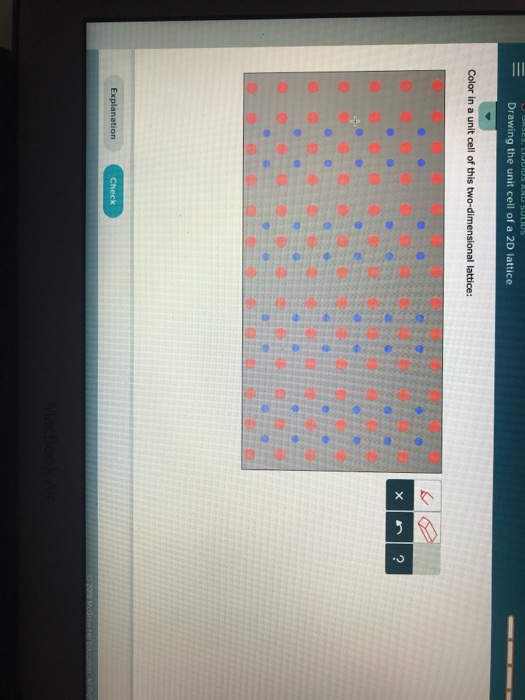
Drawing The Unit Cell Of A 2D Lattice
Drawing The Unit Cell Of A 2D Lattice - Web in a simple cubic lattice, the unit cell that repeats in all directions is a cube defined by the centers of eight atoms, as shown in figure 10.49. Find volume of unit cell: If regularly distributed, we can define a unit cell that includes the gap, as we have in drawing 11.17 a. Web any parallelepiped that connects lattice points defines a valid unit cell, and there are an infinite number of choices for drawing these. It is used to visually simplify the crystalline patterns solids arrange themselves in. The two vectors, t1 and t2 and the lattice they create describe how the unit cell repeats to make the entire tile pattern. \[\frac{2 atom mo}{unit cell}(\frac{1mol mo}{6.02x10^{23}atoms})(\frac{95.95g\: A unit cell shows the locations of lattice points repeating in all directions. Web figure 11.17 shows the two possibilities: Atoms at adjacent corners of this unit cell contact each other, so the edge length of this cell is. Unit cells in two dimensions. If regularly distributed, we can define a unit cell that includes the gap, as we have in drawing 11.17 a. Crystall lattices and unit cells. This small portion when repeated can generate the whole lattice and is called the “unit cell” and it could be larger than the primitive cell unit cell: \[\frac{2 atom mo}{unit. A unit cell shows the locations of lattice points repeating in all directions. The unit cells differ in their relative locations or orientations within the lattice, but they are all valid choices because repeating them in any direction fills the overall pattern of dots. When the unit cell repeats itself, the network is called a lattice. Web in a simple. \[\frac{2 atom mo}{unit cell}(\frac{1mol mo}{6.02x10^{23}atoms})(\frac{95.95g\: Web about press copyright contact us creators advertise developers terms privacy policy & safety how youtube works test new features nfl sunday ticket press copyright. The gaps may be either regularly (11.17 a) or randomly (11.17 b) distributed. It is very cumbersome to draw entire lattices in 3d so some small portion of the lattice,. As with the previous definition of unit cell, each unit cell contains one lattice point (1⁄4 + 1⁄4 + 1⁄4 +. The unit cells differ in their relative locations or orientations within the lattice, but they are all valid choices because repeating them in any direction fills the overall pattern of dots. Web figure 11.17 shows the two possibilities: Web. A a a unit cell of a. \[\frac{2 atom mo}{unit cell}(\frac{1mol mo}{6.02x10^{23}atoms})(\frac{95.95g\: Find diagonal of face b Web about press copyright contact us creators advertise developers terms privacy policy & safety how youtube works test new features nfl sunday ticket press copyright. As with the previous definition of unit cell, each unit cell contains one lattice point (1⁄4 + 1⁄4. The two vectors, t1 and t2 and the lattice they create describe how the unit cell repeats to make the entire tile pattern. Unit cells in two dimensions. \[\frac{2 atom mo}{unit cell}(\frac{1mol mo}{6.02x10^{23}atoms})(\frac{95.95g\: Web any parallelepiped that connects lattice points defines a valid unit cell, and there are an infinite number of choices for drawing these. Web figure 11.17 shows. Find diagonal of face b It is very cumbersome to draw entire lattices in 3d so some small portion of the lattice, having full symmetry of the lattice, is usually drawn. Web about press copyright contact us creators advertise developers terms privacy policy & safety how youtube works test new features nfl sunday ticket press copyright. The two vectors, t1. Crystall lattices and unit cells. Find diagonal of face b \[\frac{2 atom mo}{unit cell}(\frac{1mol mo}{6.02x10^{23}atoms})(\frac{95.95g\: It is very cumbersome to draw entire lattices in 3d so some small portion of the lattice, having full symmetry of the lattice, is usually drawn. Web about press copyright contact us creators advertise developers terms privacy policy & safety how youtube works test new. A a a unit cell of a. Find diagonal of face b Atoms at adjacent corners of this unit cell contact each other, so the edge length of this cell is. When the unit cell repeats itself, the network is called a lattice. This small portion when repeated can generate the whole lattice and is called the “unit cell” and. \[\frac{2 atom mo}{unit cell}(\frac{1mol mo}{6.02x10^{23}atoms})(\frac{95.95g\: Find diagonal of face b The two vectors, t1 and t2 and the lattice they create describe how the unit cell repeats to make the entire tile pattern. Find volume of unit cell: The unit cells differ in their relative locations or orientations within the lattice, but they are all valid choices because repeating them. It is very cumbersome to draw entire lattices in 3d so some small portion of the lattice, having full symmetry of the lattice, is usually drawn. When the unit cell repeats itself, the network is called a lattice. \[\frac{2 atom mo}{unit cell}(\frac{1mol mo}{6.02x10^{23}atoms})(\frac{95.95g\: The two vectors, t1 and t2 and the lattice they create describe how the unit cell repeats to make the entire tile pattern. A unit cell shows the locations of lattice points repeating in all directions. Find volume of unit cell: Atoms at adjacent corners of this unit cell contact each other, so the edge length of this cell is. Let us begin our investigation of crystal lattice structure and unit cells with the most straightforward structure and the most basic unit cell. A a a unit cell of a. The unit cells differ in their relative locations or orientations within the lattice, but they are all valid choices because repeating them in any direction fills the overall pattern of dots. Web figure 11.17 shows the two possibilities: Unit cells in two dimensions. A unit cell is the most basic and least volume consuming repeating structure of any solid. Web any parallelepiped that connects lattice points defines a valid unit cell, and there are an infinite number of choices for drawing these. The gaps may be either regularly (11.17 a) or randomly (11.17 b) distributed. It is used to visually simplify the crystalline patterns solids arrange themselves in.
CRYSTAL LATTICE AND UNIT CELL YouTube

Schematic diagram of a 2D diamondoctagon lattice model. The unit cells
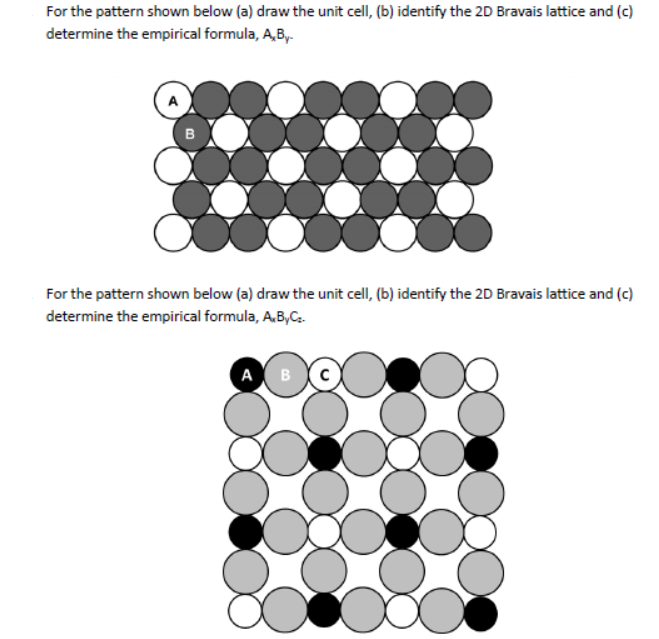
Drawing the Unit Cell of a 2d Lattice
Solved Drawing the unit cell of a 2D lattice
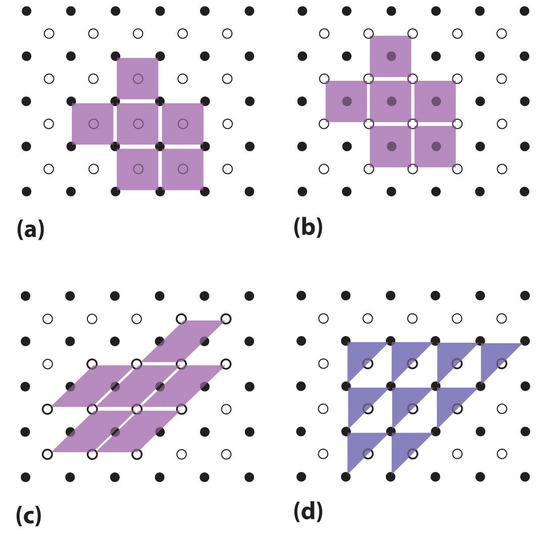
10.3 Lattices and Unit Cells Chemistry LibreTexts

Crystal Lattice — Structure & Formation Expii

2D lattice made of framelike diamondsquare unit cells. a Lattice. b

Drawing the Unit Cell of a 2d Lattice
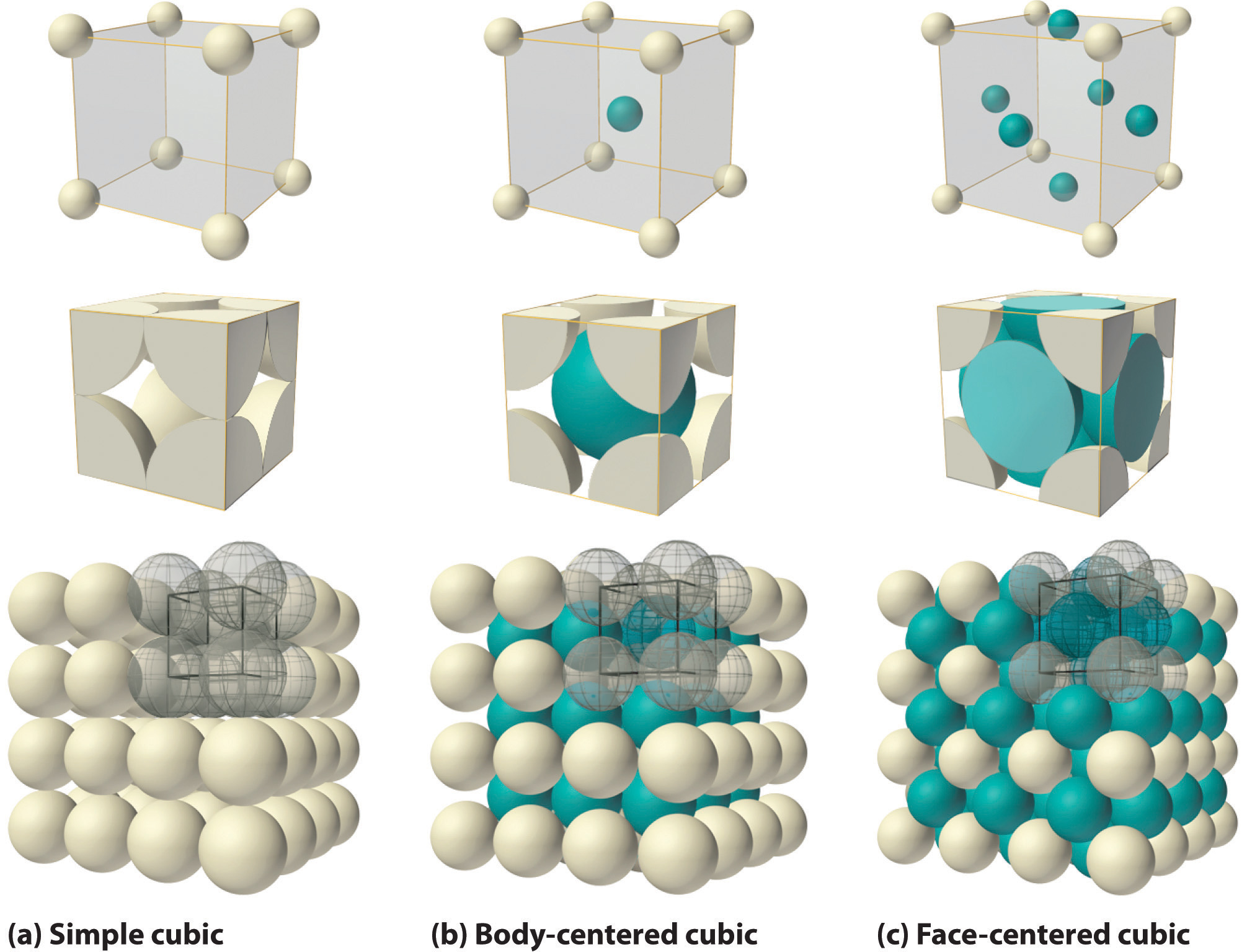
12.1 Crystal Lattices and Unit Cells Chemistry LibreTexts
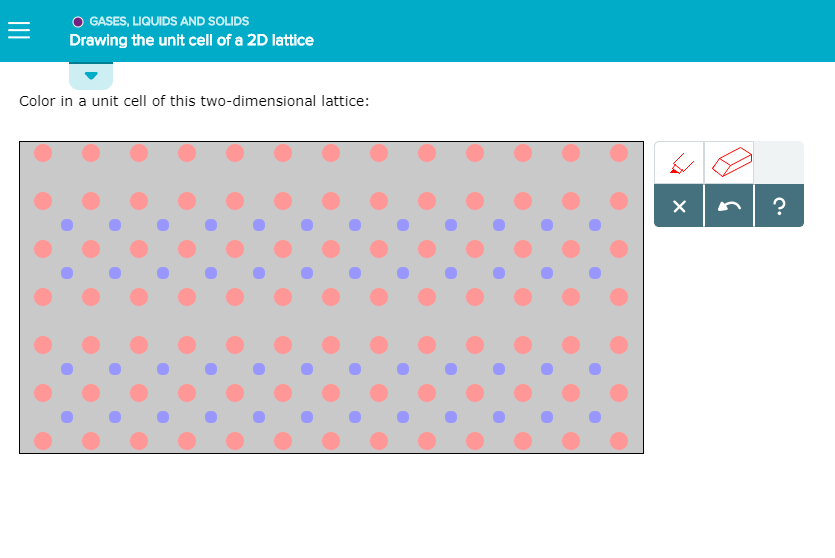
Drawing the Unit Cell of a 2d Lattice
As With The Previous Definition Of Unit Cell, Each Unit Cell Contains One Lattice Point (1⁄4 + 1⁄4 + 1⁄4 +.
If Regularly Distributed, We Can Define A Unit Cell That Includes The Gap, As We Have In Drawing 11.17 A.
Find Diagonal Of Face B
Crystall Lattices And Unit Cells.
Related Post: