How To Draw Derivatives
How To Draw Derivatives - The second derivative of f is. It explains how to graph polynomial functions using the signs of the first. Web so i feel calling the middle graph f, calling the left graph f prime, and calling the right graph the second derivative. Web from the table, we see that f has a local maximum at x = − 1 and a local minimum at x = 1. The winner will be announced in august. As always, we are here to help. We will use that understanding a. For example, d dx d d x (x2) ( x 2) will graph the derivative of x2 x 2 with respect to x x, or d dx d d x (sinx) ( s i n x) will graph the derivative of sinx s i n x with respect to x x. 4.5.4 explain the concavity test for a function over an open interval. The canadian alternative reference rate working group (carr) has published new information 1 relating to the. Web draw graph of derivative: You can use d dx d d x or d dy d d y for derivatives. If we look at our graph above, we notice that there are a lot of sharp points. Web this calculus video tutorial explains how to sketch the derivatives of the parent function using the graph f(x). If so, delete. Web graph of derivative to original function. At any sharp points or cusps on f (x) the derivative doesn't exist. The point x = a determines an absolute maximum for function f if it. In this section we will use our accumulated knowledge of derivatives to identify the most important qualitative features of graphs \ (y=f (x)\text {.}\) Learn for. This video contains plenty of examples and. If we look at our graph above, we notice that there are a lot of sharp points. Start practicing—and saving your progress—now: Place a straight object like your pencil on your original function’s curve where the points in “step 1” lie, to mimic a tangent line. A line has a positive slope if. A line has a negative slope if it is decreasing from left to right. One of the most obvious applications of derivatives is to help us understand the shape of the graph of a function. This means we have possible maximums or minimums at these points. In the graph shown, the function is increasing on the left of the first. Web 👉 learn all about the applications of the derivative. 4.5.1 explain how the sign of the first derivative affects the shape of a function’s graph.; If the tangent line is vertical. This means we have possible maximums or minimums at these points. Place a straight object like your pencil on your original function’s curve where the points in “step. Slopes of lines and their defining characteristics. 4.5.1 explain how the sign of the first derivative affects the shape of a function’s graph.; The second derivative of f is. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Web if there's a break or a hole in f (x) the derivative doesn't exist there. One of the most obvious applications of derivatives is to help us understand the shape of the graph of a function. It is where the graph has a positive gradient. Slopes of lines and their defining characteristics. The second derivative is zero at x = 0. In this section we will use our accumulated knowledge of derivatives to identify the. Place a straight object like your pencil on your original function’s curve where the points in “step 1” lie, to mimic a tangent line. 4.5.2 state the first derivative test for critical points.; If so, delete this step. In the graph shown, the function is increasing on the left of the first turning point. Differentiation allows us to determine the. The derivative is the slope of the tangent line at a particular point on the graph. Web if there's a break or a hole in f (x) the derivative doesn't exist there. The second derivative is zero at x = 0. It is where the graph has a positive gradient. As always, we are here to help. The canadian alternative reference rate working group (carr) has published new information 1 relating to the. One of the most obvious applications of derivatives is to help us understand the shape of the graph of a function. Web from the table, we see that f has a local maximum at x = − 1 and a local minimum at x. A function is increasing if it is going up from left to right. At any sharp points or cusps on f (x) the derivative doesn't exist. The second derivative of f is. 4.5.4 explain the concavity test for a function over an open interval. The derivative is the slope of the tangent line at a particular point on the graph. Web this calculus video tutorial explains how to sketch the derivatives of the parent function using the graph f(x). Web graph of derivative to original function. One of the most obvious applications of derivatives is to help us understand the shape of the graph of a function. F ″ (x) = 6x. The kinds of things we will be searching for in this section are: This is because the slope of a vertical line is undefined. A function f(x) is said to be differentiable at a if f. F ′ (x) = lim h → 0f(x + h) − f(x) h. Web so i feel calling the middle graph f, calling the left graph f prime, and calling the right graph the second derivative. What do you notice about each pair? Let f be a function.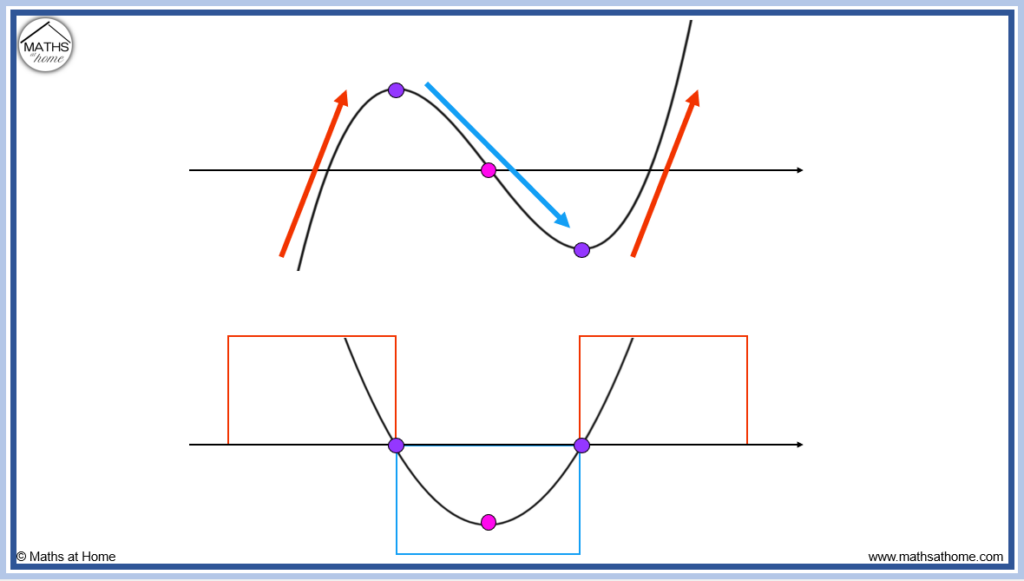
How to Sketch the Graph of the Derivative

Draw the Function given Graph of Derivative YouTube
How to Sketch the Graph of the Derivative

How to sketch first derivative and Function from graph of second
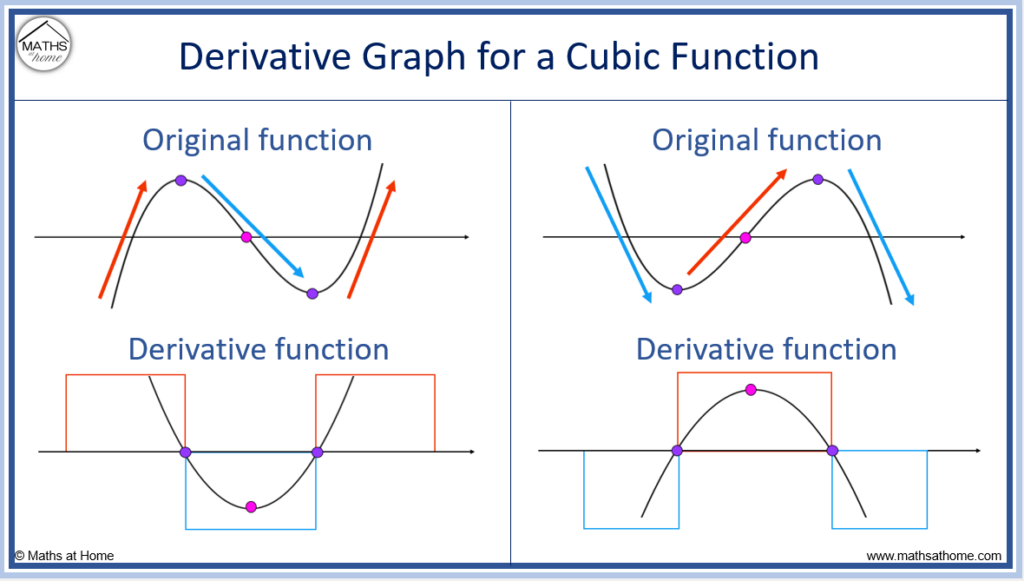
How to Sketch the Graph of the Derivative

MATH221 Lesson 009B Drawing Derivatives YouTube
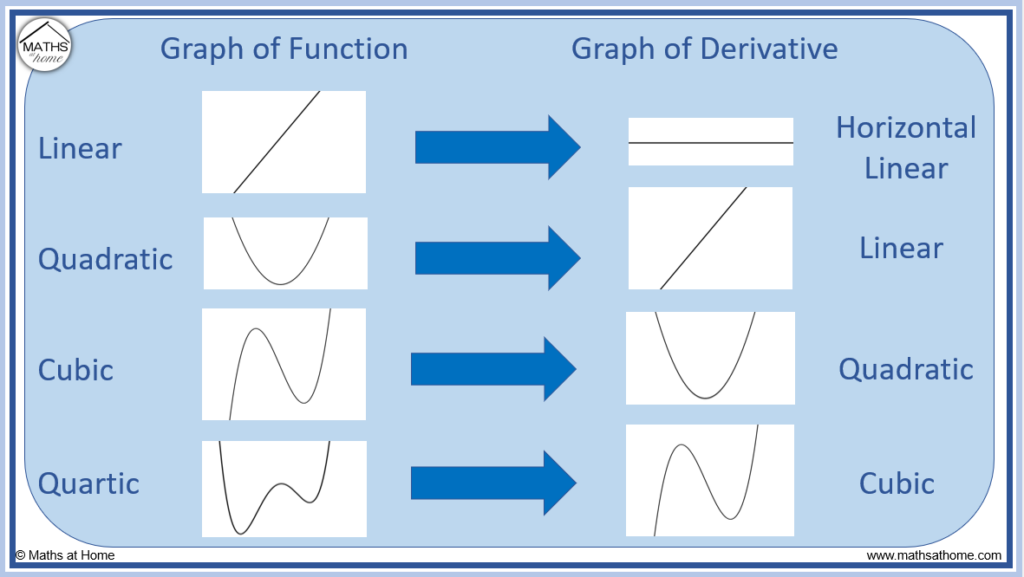
How to Sketch the Graph of the Derivative

Drawing the Graph of a Derivative YouTube
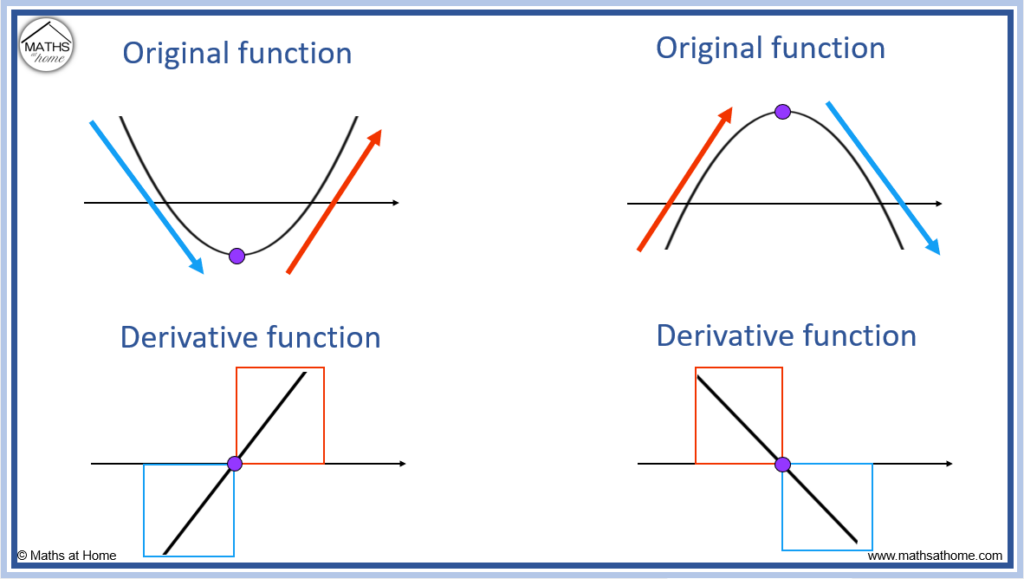
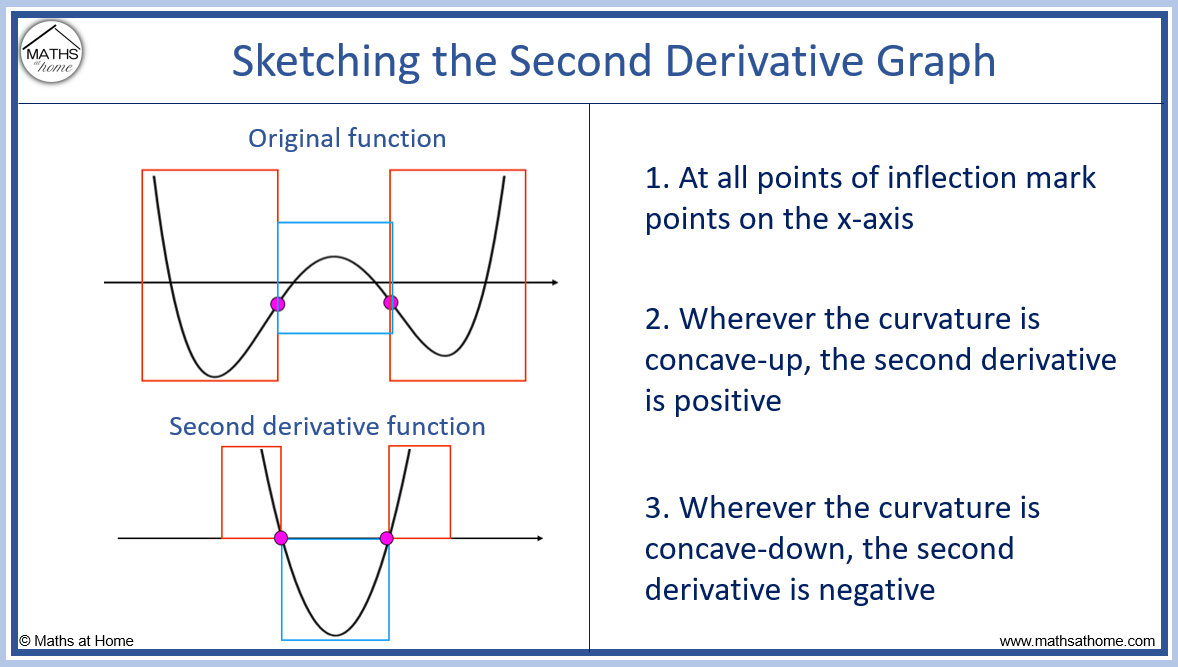
How to Sketch the Graph of the Derivative
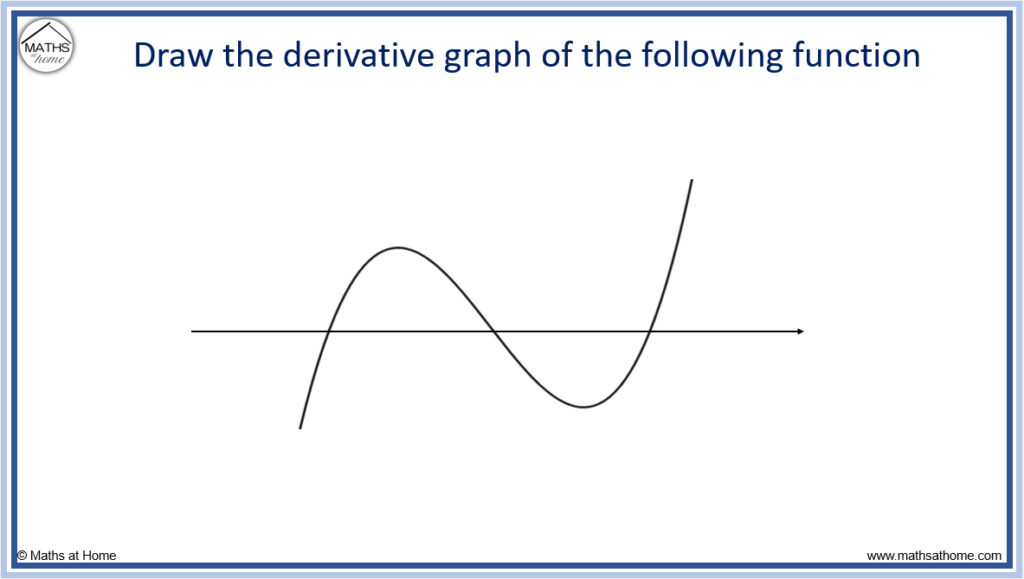
How to Sketch the Graph of the Derivative
This Video Contains Plenty Of Examples And.
The Derivative Function, Denoted By F ′, Is The Function Whose Domain Consists Of Those Values Of X Such That The Following Limit Exists:
The Application Portal Will Be Open From May 13Th Until June 14Th.
It Explains How To Graph Polynomial Functions Using The Signs Of The First.
Related Post: