Trig Antiderivatives Chart
Trig Antiderivatives Chart - Given a function \(f\), we use the notation \(f′(x)\) or \(\dfrac{df}{dx}\) to denote the derivative of \(f\). Web the table below shows you how to differentiate and integrate 18 of the most common functions. One of the most important types of motion in physics is simple harmonic motion, which is associated with such systems as an object with mass oscillating on a spring. Web functions involving trigonometric functions are useful as they are good at describing periodic behavior. For a longer list of antiderivative formulas, see your textbook. If the power n of cosine is odd (n = 2k + 1), save one cosine factor and use cos2(x) = 1 express the rest of the factors in terms of sine: Explain the terms and notation used for an indefinite integral. F (x) = xn xn+1 (if n 6= 1) f(x) = n+1 + c. Web finding antiderivatives of polynomials is generally not too hard. When you learn about the fundamental theorem of calculus, you will learn that the antiderivative has a very, very important property. From wikipedia, the free encyclopedia. Web in the video, we work out the antiderivatives of the four remaining trig functions. These properties allow us to find antiderivatives of more complicated functions. 1 f (x) = x = f(x) = ln(jxj) + x c f. Find the general antiderivative of a given function. Web those would be derivatives, definite integrals, and antiderivatives (now also called indefinite integrals). We just need to use the rule \begin{gather*} \text{if } f(x) = x^n \text{ then } f(x) = \frac{1}{n+1} x^{n+1} + c. One of the most important types of motion in physics is simple harmonic motion, which is associated with such systems as an object with. State the power rule for integrals. Complicated functions can be computed from these using techniques like. Web list of derivatives of trig & inverse trig functions. For antiderivatives involving both exponential and trigonometric functions, see list of integrals of exponential functions. Web those would be derivatives, definite integrals, and antiderivatives (now also called indefinite integrals). State the power rule for integrals. Let us go through the important antiderivative rules in the sections below. The antiderivatives of tangent and cotangent are easy to. 1 f (x) = x = f(x) = ln(jxj) + x c f. For antiderivatives involving both exponential and trigonometric functions, see list of integrals of exponential functions. For a longer list of antiderivative formulas, see your textbook. The remaining four are left to you and will follow similar proofs for the two given here. Sometimes, it may be possible to use one of these standard forms directly. Web the table below shows you how to differentiate and integrate 18 of the most common functions. Web not to. Find the general antiderivative of a given function. Parts, partial fractions, trig substitution, etc. Web list of derivatives of trig & inverse trig functions. Sometimes, it may be possible to use one of these standard forms directly. Here we introduce notation for. If the power n of cosine is odd (n = 2k + 1), save one cosine factor and use cos2(x) = 1 express the rest of the factors in terms of sine: Web these are the antiderivative formulas you should memorize for math 3b. Web we’ll start this process off by taking a look at the derivatives of the six. Web functions involving trigonometric functions are useful as they are good at describing periodic behavior. For a longer list of antiderivative formulas, see your textbook. Some of the following trigonometry identities may be needed. Explain the terms and notation used for an indefinite integral. State the power rule for integrals. (you will obtain them in the exercises.) integral rule. Sometimes, it may be possible to use one of these standard forms directly. Find the general antiderivative of a given function. $\int \cos x\ dx = \sin x + c$. Web not to keep you in suspense, here are the antiderivatives of all six trigonometric functions. For antiderivatives involving both exponential and trigonometric functions, see list of integrals of exponential functions. Web these rules can be used for the antidifferentiation of algebraic functions, exponential function, trigonometric functions, hyperbolic functions, logarithmic function, and constant function. The antiderivatives of tangent and cotangent are easy to. $\int \cos (ax+b) dx = \frac {1} {a} \sin (ax+b) + c$. Web. The remaining four are left to you and will follow similar proofs for the two given here. Given a function \(f\), we use the notation \(f′(x)\) or \(\dfrac{df}{dx}\) to denote the derivative of \(f\). Complicated functions can be computed from these using techniques like. Two of the derivatives will be derived. These properties allow us to find antiderivatives of more complicated functions. For a complete list of antiderivative functions, see lists of integrals. When you learn about the fundamental theorem of calculus, you will learn that the antiderivative has a very, very important property. Web we’ll start this process off by taking a look at the derivatives of the six trig functions. The following is a list of integrals (antiderivative functions) of trigonometric functions. Web recall the definitions of the trigonometric functions. $\int \sin x\ dx =. From wikipedia, the free encyclopedia. Web list of derivatives of trig & inverse trig functions. $\int \cos x\ dx = \sin x + c$. Explain the terms and notation used for an indefinite integral. On other occasions, some manipulation will be needed first.
Antiderivatives of Trig functions YouTube

Basic Antiderivatives of Trigonometric Functions YouTube

6.1b Antiderivatives of Trig Functions AP Calculus YouTube
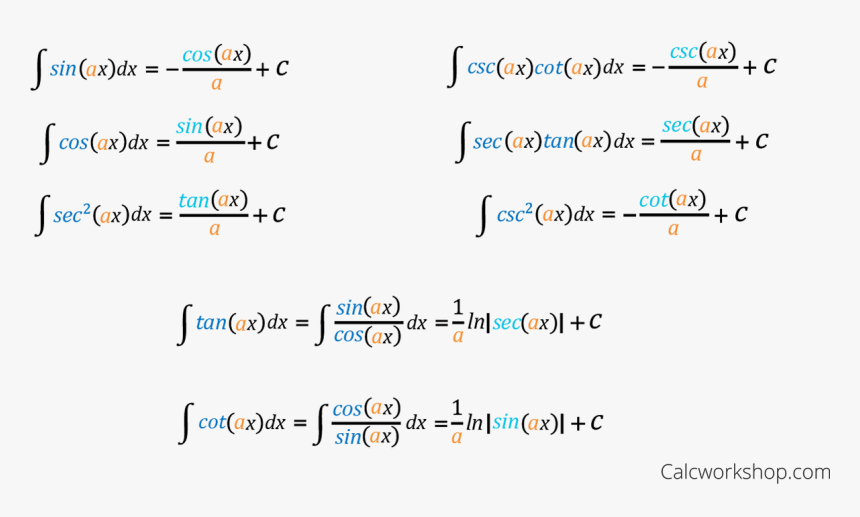
Rules For Integrating Trig Functions Antiderivative Trig Chart, HD

6.8 Finding Antiderivatives and Indefinite Integrals (Part 5

Trig Antiderivatives
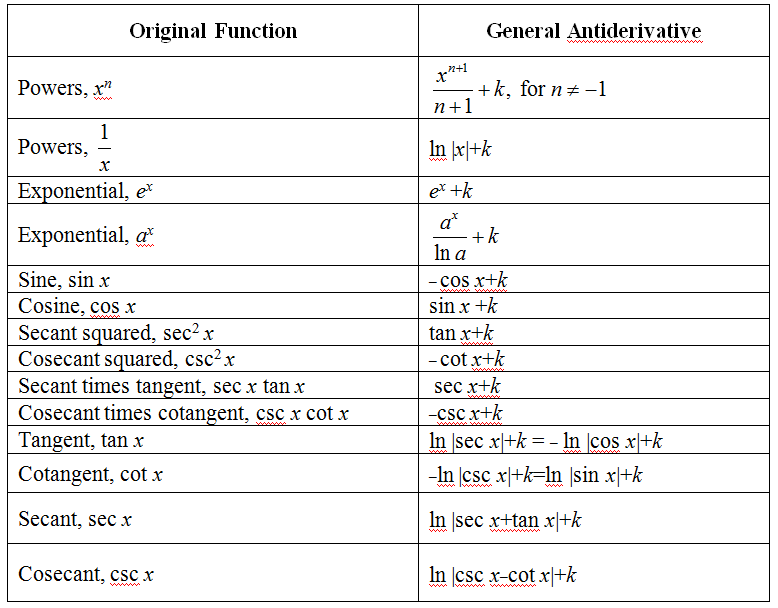
Common Trig Derivatives And Integrals Slidesharetrick 302

Antiderivative Rules List, Formulas, Examples What are

4.82 Some trigonometric antiderivatives YouTube

Common Trig Derivatives And Integrals Slidesharetrick 302
Web The Following Is A List Of Integrals ( Antiderivative Functions) Of Trigonometric Functions.
It Is Assumed That You Are Familiar With The Following Rules Of Differentiation.
The Antiderivatives Of Tangent And Cotangent Are Easy To.
Find The General Antiderivative Of A Given Function.
Related Post: