Laplace Transform Chart

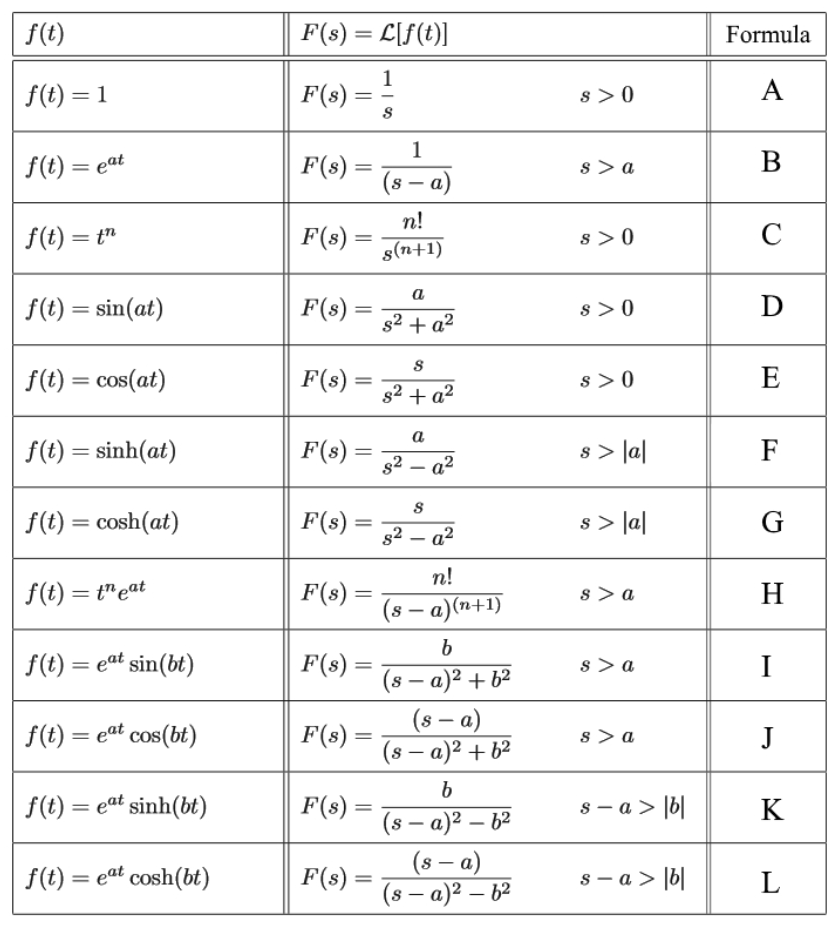
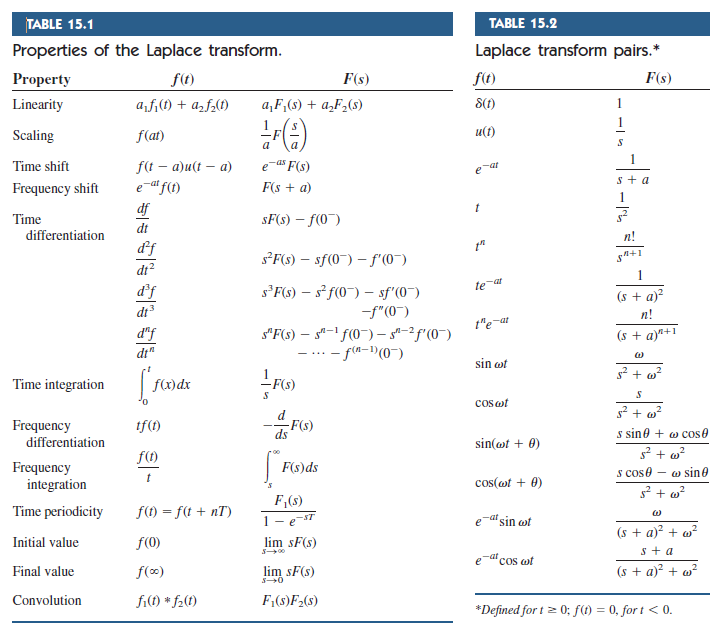
Laplace Transform Chart - The laplace transform maps a function of t t to a function of s. Web table of laplace transforms and inverse transforms f(t) = l¡1ff(s)g(t) f(s) = lff(t)g(s) tneat n! Web laplace transform of the unit step function. Introduction to the unit step function and its laplace transform. Γ(t) = ∫∞ 0 e−ττt−1dτ, erf(t) = 2 π−−√ ∫t 0 e−τ2dτ, erfc(t) = 1 − erf(t). Recall the definition of hyperbolic functions. Web table of laplace transforms. U(t−a) e−as s a≥0 11. 1 √ t r π s 10. Y b, satisfying the boundary conditions u(x, 0) = u(x, b) = 0 for 0 < x < a and u(0, y) = 0 and u(a, y) = f(y) for 0 y b has the general form.

Laplace Transforms Table Method Examples History of Laplace Transform

Web ect sin(at) (s − c)2 + a2. 1 √ t r π s 10. Cosh(at) s s2 −a2, s > |a| 9. It can also be used to solve certain improper integrals like the dirichlet integral. Web cn = f(x) sin dx and kn = g(x) sin dx.

Solved 4 The Laplace transforms of some common functions.

In what cases of solving odes is the present method preferable to that in chap. 1 √ t r π s 10. Please memorize the following table of laplace transforms. S > a eat cosbt s¡a (s¡a)2 +b2; Sn+1 (11) tx (x 1 2r) ( x+ 1) sx+1 (12) sinkt k s2 + k2 (13) coskt s s2 + k2.

Laplace Transform Cheat Sheet Electrical and Electronics Engineering

Cosh(at) s s2 −a2, s > |a| 9. Recall the definition of hyperbolic functions. Web laplace transform of the unit step function. U(t−a) e−as s a≥0 11. Please memorize the following table of laplace transforms.

Laplace Transform Full Formula Sheet

Recall the definition of hyperbolic functions. Web table of laplace transforms f(t) l(f(t)) or f(s) 1. Eat sin(bt) b (s −a)2 +b2, s. Y b, satisfying the boundary conditions u(x, 0) = u(x, b) = 0 for 0 < x < a and u(0, y) = 0 and u(a, y) = f(y) for 0 y b has the general form..

Laplace table

First, suppose that f is the constant 1, and has no discontinuity at t = 0. What property of the laplace transform is crucial in solving odes? U(t−a) e−as s a≥0 11. Tp, p > −1 γ(p +1) sp+1, s > 0 5. Eat 1 s −a, s > a 3.

Laplace transform chart subtitlemoney

The laplace transform maps a function of t t to a function of s. Sn+1, s > 0 4. Sinh(at) a s2 −a2, s > |a| 8. Web this section is the table of laplace transforms that we’ll be using in the material. Web table of elementary laplace transforms f(t) = l−1{f(s)} f(s) = l{f(t)} 1.

Calculating laplace transforms StudyPug

The laplace transform maps a function of t t to a function of s. Ect cos(at) s − c. S > a eat cosbt s¡a (s¡a)2 +b2; Web table of laplace transforms. Eatsinkt k (s−a)2 +k2 8.

Laplace transform chart hipfreeloads

Et + e t et e t. Web table of laplace transforms. S > a eat sinbt b (s¡a)2 +b2; (s − c)2 + a2. Cosh(at) s s2 −a2, s > |a| 9.

Laplace transform table ladercosmic

We give as wide a variety of laplace transforms as possible including some that aren’t often given in tables of laplace transforms. In the next section we will show how these transforms can be used to sum infinite series and to solve initial value problems for ordinary differential equations. Γ(t) = ∫∞ 0 e−ττt−1dτ, erf(t) = 2 π−−√ ∫t 0.

Solved Use Laplace Transforms To Solve The Initial Value

Web find the laplace transform of \(f(t)=e^{at}\), where \(a\) is a constant. Linear algebra (exercises) back matter. Sin(at) a s2 +a2, s > 0 6. Tp, p > −1 γ(p +1) sp+1, s > 0 5. Web table of elementary laplace transforms f(t) = l−1{f(s)} f(s) = l{f(t)} 1.

Sinh(At) A S2 −A2, S > |A| 8.

Et + e t et e t. Web table of laplace transforms and inverse transforms f(t) = l¡1ff(s)g(t) f(s) = lff(t)g(s) tneat n! Web this section is the table of laplace transforms that we’ll be using in the material. Of the video sal begins integration.

Eatcoskt S−A (S−A)2 +K2 9.

Want to join the conversation? Eat sin(bt) b (s −a)2 +b2, s. Web table of elementary laplace transforms f(t) = l−1{f(s)} f(s) = l{f(t)} 1. Web 25 rows find the laplace transform of various time functions in this table.

1 √ T R Π S 10.

U(t−a) e−as s a≥0 11. Web what are the steps of solving an ode by the laplace transform? Be careful when using “normal” trig function vs. First, suppose that f is the constant 1, and has no discontinuity at t = 0.

Γ(T) = ∫∞ 0 E−Ττt−1Dτ, Erf(T) = 2 Π−−√ ∫T 0 E−Τ2Dτ, Erfc(T) = 1 − Erf(T).

The laplace transform maps a function of t t to a function of s. See examples, properties, inverse laplace, convolution and more. Want to join the conversation? L 0 l n⇡↵ z 0 l.